Processing

This page contains a few Processing sketches I've made. Note that I've made a ton of these, but I only display a select few here. Every sketch on this page was made entirely by me and is unrelated to my study. I make these as a hobby and a way to keep my programming skills sharp.

Portfolio Overview

Overview

All projects are listed together on one page; This page. You can choose to scroll through or use the provided quick-navigation on the right to go to a specific project.

Golden Ratio Circles

Golden Ratio Circles GIF by Joep Eijkemans (Inspired by Wujek_Greg)

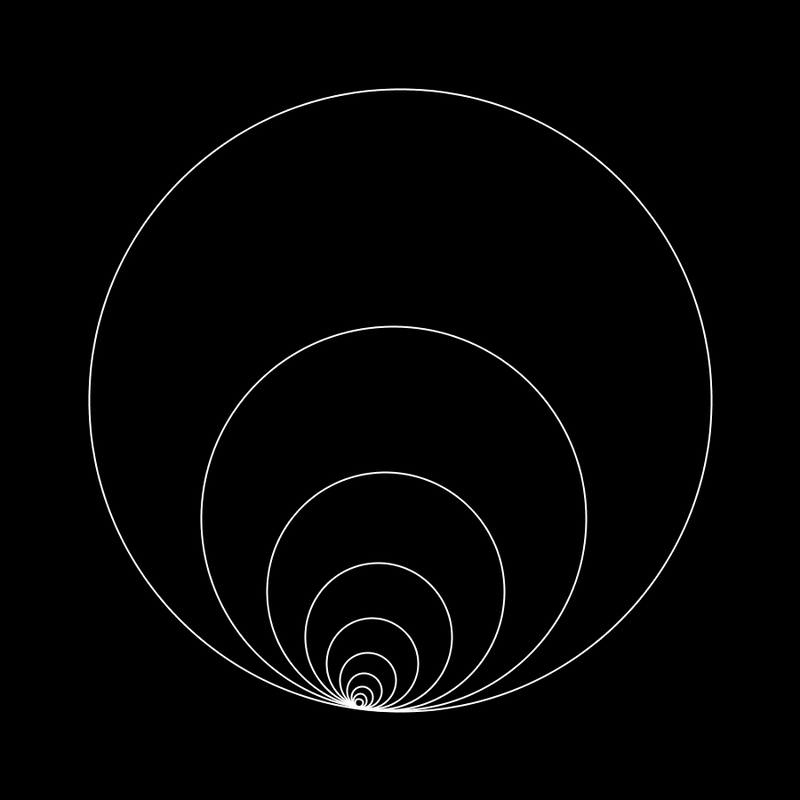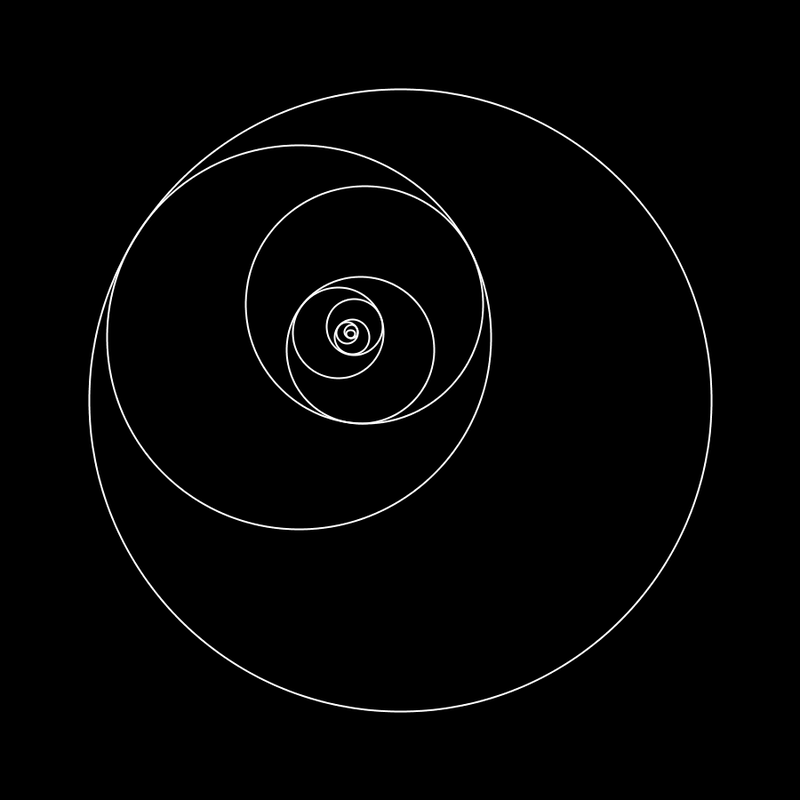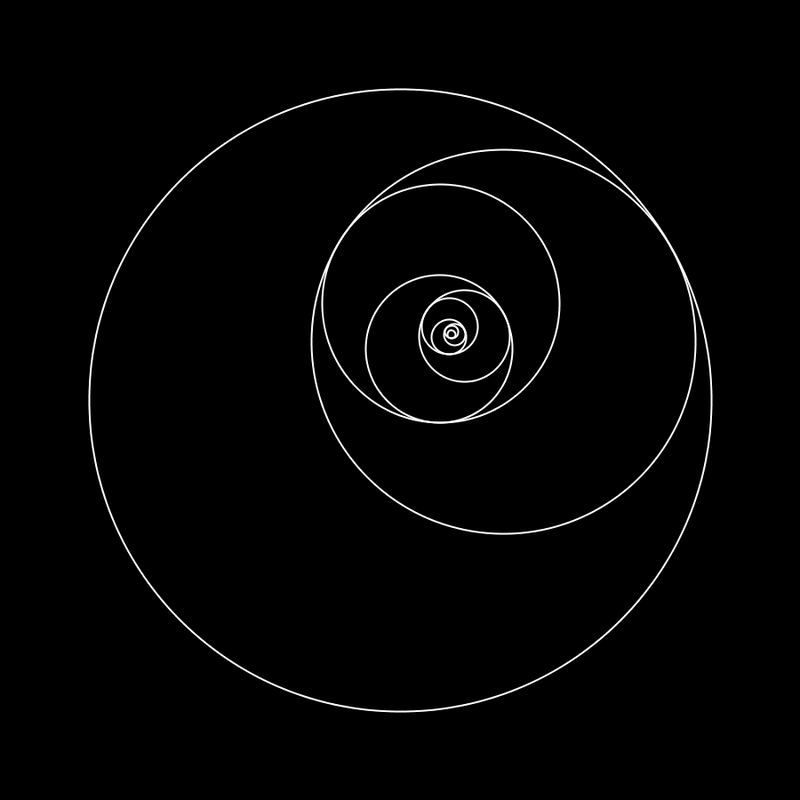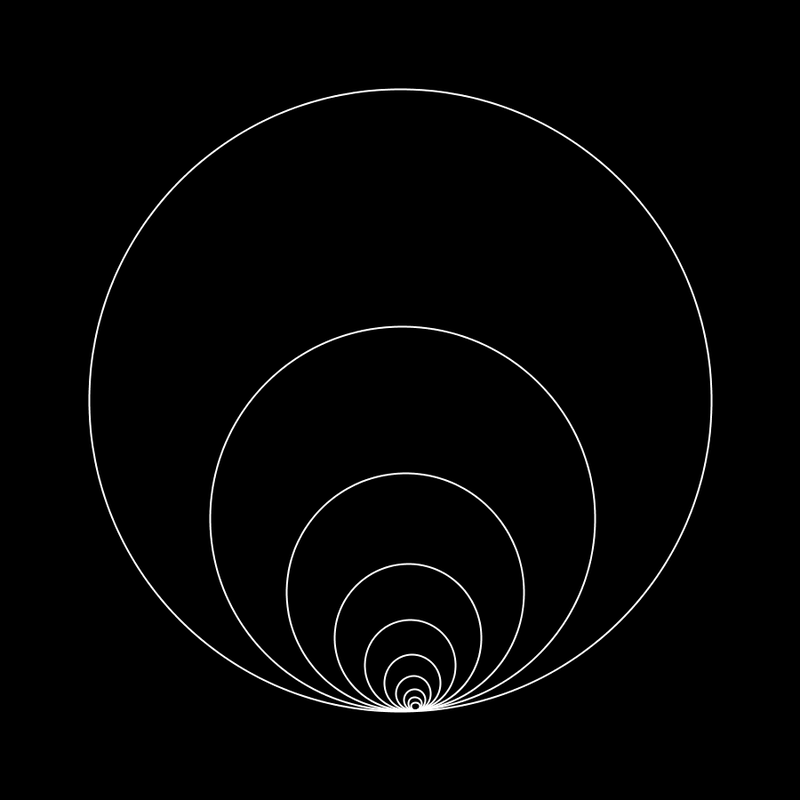
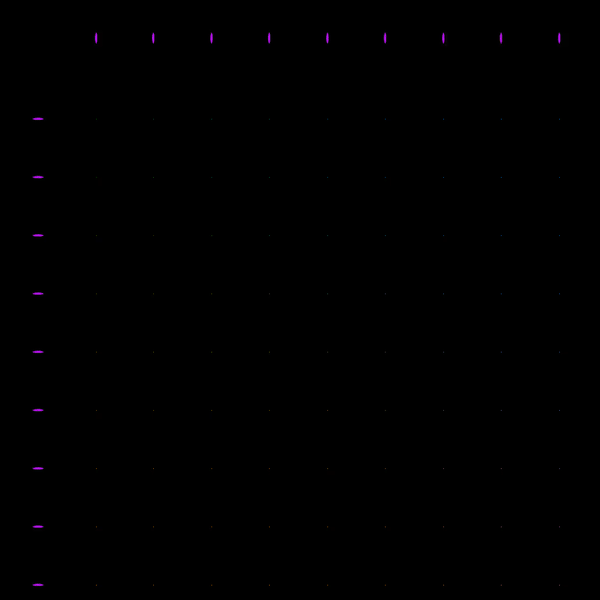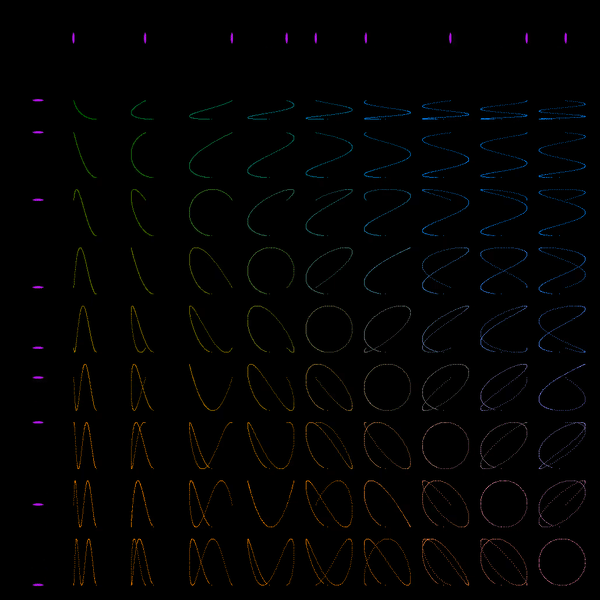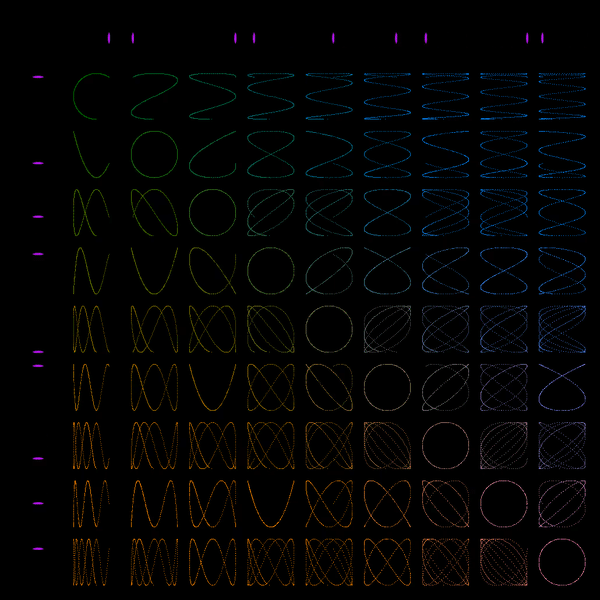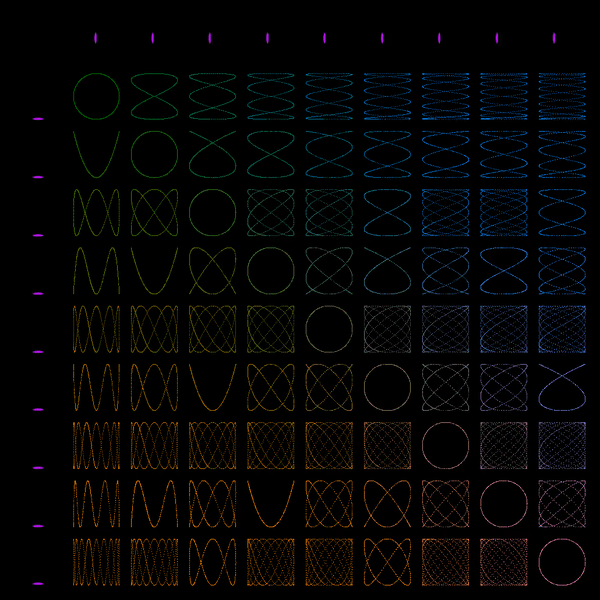
I initially made this after I was inspired by an Instagram post showing a similar image created by "Wujek_Greg". It's a really simple program (only 30 lines of code or something), which creates a series of circles that, together, illustrate the beauty created by the so-called "Golden Ratio". The Golden Ratio is an irrational, non-terminating number (approx. 1.61803398875). It is said that things that contain many elements with an 1 : 1.618 ratio are considered beautiful. Every circle in my program is scaled with the inverse of this ratio relative to its parent. The smaller circles rotate faster than the larger ones, creating a nice 'swoop' every loop.

I posted the result on r/oddlysatisfying on Reddit, and it went viral. Within 24 hours the post received over 42 000 upvotes. It got reposted on many other communities as well. Including: r/WoahDude (29 000 upvotes), r/LoadingIcon (1300 upvotes), r/EducationalGifs (27 200 views) and many others. Within an hour after posting it was also shared on 9GAG and Instagram.

Note that there are many more Reddit communities and other social media posts. It got a bit out of my control and I didn't get credited or informed everywhere where it was shared.

Source code

Also note that I shared my code via GitHub and I still receive mentions about people who made something similar using my code as a basis. Have a look at this example. Check out my code by clicking the button below.

View code

Paint By Number

Paint By Number Processing Sketch example 1

Do you remember those paint-by-number paintings? Turns out that there are advanced alternatives of those as well. Large paintings with 30 – 40 colors and super tiny paint regions. My girlfriend loves those. So, I wrote a program that could turn any image into a paint-by-number painting.

It works as follows: First you choose a picture / image. You then click on certain parts of this image to create a color palette. By default, the color palette already contains white, grey, black, red, green & blue. The color of every pixel you click is then added to the palette.

Paint By Number Processing Sketch example 2

You run the program, and it matches every pixel in the image and finds the most similar color in the color palette. The image essentially gets turned into a version of itself that exclusively consists of colors from the preselected palette.

I then do some smoothing to remove single pixels. And then I apply an edge-detection kernel to mark the edges of the paint regions. It colors the lines a shade of black / grey that has not been, and cannot be, selected as a palette color.

I've not yet added the functionality that prints the numbers of every color in the respective paint regions.

Paint By Number Processing Sketch example 3

The program is also able to color the painting itself, since it already knows what colors are supposed to go where. That's how I created the images that decorate this section.

If you wish to play around with this program yourself, or even modify the code. You can download it by pressing the button below. Note that it's only available for Windows at the moment.

Click on the button on the left to download the compiled program.
Click on the button on the right to view the source code on GitHub.

Download program

Download

Source code

View code

Lissajous Curve Table

Lissajous Curve Table GIF

This program was made after a post I saw on Reddit. Since I had struggled with basic sine functions in the past, I felt like this would be a nice method of gaining a bit more insight, as well as to create a beautiful GIF.

What I've made is called a Lissajous Curve Table, named after Jules Antoine Lissajous. It's basically just a matrix of sine functions. Each iteration has a higher frequency. The tables create patters by following the point of the X coordinate from the horizontal row and the Y coordinate from the vertical column.

Or, to formulate it more scientifically correct: "Each element in the matrix is created by following a point which participates in two perpendicular harmonic functions simultaneously". Not to be confused with a spirograph, which is typically enclosed by a circular boundary. As the GIF illustrates, Lissajous Curves are enclosed by a rectangular boundary.

I then added some nice colors to each element in the matrix to make it more aesthetically appealing.

Source code

Click the button below to look at the code used to create the image above on GitHub.

View code

Sudoku Solving Algorithm

This is a project I did during the corona crisis lockdown to help against the boredom. It all started when I told my dad that sudoku puzzles are easy, since everything you need for the answer is always already there, and there's usually a clear path since whatever you fill in unlocks new information. He then said that I should make one, but I'm not really one for tasks that can be easily automated. So instead, I wrote a program that can solve (almost) any sudoku.

The program works as follows: It first generates an array of 81 instances of the class 'Field'. Each instance has a number of variables: X & Y coordinates, the value it has, whether or not this value is fixed, and an array of potential options that could fit that field, which is always 1 – 9 at this point.

We then fill in the values of the sudoku that we're trying to solve. If the field has some value, we set it to fixed and remove all potential options. The number of empty fields is the same as the amount of iterations the program needs to solve the sudoku. The program will start a new iteration after finding a single solution, since filling in multiple fields during a single iteration could cause incorrect answers.

We then start looking for possible solutions for every field, using a number of strategies of increasing complexity.

Sudoku solving strategy 1: Only option

Strategy 1: Only option

First, we determine which options there are for each field. Every field is compared to every other field in the same row, column or 3x3 square. If any of those fields already contain a fixed number, this number is removed from the potential options for said field.

We then check if there exists a field which only has one possible option left, if yes, set the value of that field to that solution. If we find a solution, we fill it in, set it to fixed and start a new iteration.

For example: Let's say the program reads the sudoku like it is presented on the left. After simply deducting every number that's also present in the same row, column or 3x3 box, the first field on the second row only has one option left: 4.

In this case, this action even unlocks the next solution via this strategy: The sixth field in this column can now only be 3.

This strategy may not find a lot of solutions, but it is quick and intuitive. It is the first strategy we apply, so that if this strategy does find a solution, we haven't wasted our time on the more complicated, time-consuming strategies.

Sudoku solving strategy 2: Solution exclusivity

Strategy 2: Solution exclusivity

If the previous step didn’t find any solution, we apply a different strategy that I call "Solution exclusivity". This is probably the most common strategy for basic sudokus. Here's how it works: The potential solutions for each field is compared with those of all other fields in the same row, column or 3x3 box. If a certain field has one specific solution, that is not an option anywhere else in the row, column or 3x3 box, this must be the correct one for that field.

For example: Let's say you only have a sudoku like the one shown on the left. In the middle-right 3x3 box, you can find that the top-right field is supposed to be 5, even though there are still multiple options available for this field (3, 5, 6 & 8). But because the left and middle column cannot contain the number 5, and this is the only field left in this column, the solution must be 5. Most beginner & average level sudokus can be solved using just these 2 strategies.

Again, if we find an answer using this step, we fill it in and start a new iteration. Otherwise, we continue with the next strategy.

Sudoku solving strategy 3: Potential solution division

Strategy 3: Potential solution division

The last strategy we apply is what I call "Potential solution division". What it does is: It checks whether a certain array of potential solutions occurs in multiple fields. If the number of fields with a specific array of potential solutions is equal to the number of solutions in that array, every potential solution from this array can be removed from all other potential solutions arrays in a specific row, column or 3x3 box.

For example: Let's say we have a sudoku like the one shown on the left. None of our previous strategies could find an answer for any field at this point. But, using this strategy, we can find a solution on the second row.

We can see that field number 3 and 9 have the exact same array of options (7 & 8). This means that no other field could possibly have these options, since that would leave no solution for these fields. Field number 2 in this row has the potential solutions 3 and 8. But since 8 has been given to either field 3 or 9 (we don't know which yet), this field couldn't possibly be 8. This means that it must be 3.

I considered adding one more failsafe strategy at the end, but eventually decided not to do that. Some sudokus cannot be fixed by any of the abovementioned logic, but require the person making them to guess and see if their guess was correct. I could, in theory, program it such that if none of the abovementioned strategies can come to a solution, we safe the sudoku as it is now, take a field with just 2 potential solutions, pick one, and see if it works out. If not, we can try again using the other option and the back-up of the sudoku. However, I didn't feel like adding this since I consider forcing people to guess is an unfair strategy to begin with and not a satisfying method of solving a puzzle.

Source code

You can see and download my code via the link below. Note that because this was just a small hobby project, the code isn’t up to my usual standards on elements like comments and organization. But, I thought I'd make it public nonetheless.

View code